Contributed talk

Exploring Chiral Spin States in Curved Spaces: Insights from Ring Geometries
Dario Bercioux^1,2, D. Frustaglia³, and A. De Martino⁴

1 Donostia International Physics Center (DIPC), Manuel de Lardizbal 4, E-20018 San Sebastián, Spain
2 IKERBASQUE, Basque Foundation for Science, Euskadi Plaza, 5, 48009 Bilbao, Spain
3 Departamento de Fíisica Aplicada II, Universidad de Sevilla, E-41012 Sevilla, Spain
4 Department of Mathematics, City, University of London, London EC1V 0HB, United Kingdom

In this talk, I will briefly revise the problem of electron spins moving in curved spaces; particularly, I will focus on the problem of ring geometry. Successively, I will show how chiral states in circular graphene pn junctions subject to normal magnetic fields and strong proximitized spin-orbit coupling can mimic those of propagating spin carriers in semiconducting quantum rings. I will derive the effective one-dimensional Hamiltonian governing the spin dynamics of the zero modes and calculate the associated geometric phase. I will show that for a given polarity of the junction, it exists a special point in parameter space where the spin is fully polarized along the radial direction in the plane of graphene. Furthermore, I will propose an innovative quantum-Hall interferometer setup capable of readily identifying and observing these remarkable features. By leveraging this interferometer, I can gain valuable insights into the intricate nature of chiral spin states and their manifestation in ring geometries.

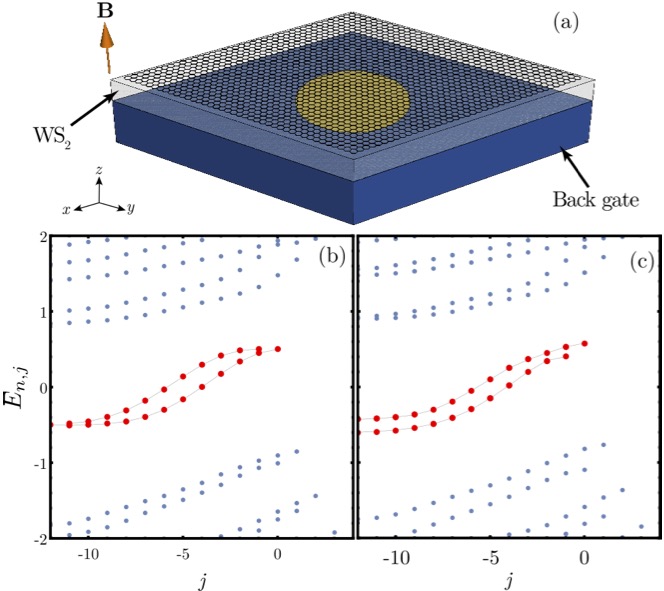
Figure 1: (a) Sketch of the system. (b) and (c) System’s spectrum with Rashba spin-orbit and Zeeman coupling, respectively.

[1] Bercioux, Frustaglia and De Martino, arXiv:2303.05833 (2023).