Contributed talk

Mach-Zehnder-like interferometry with graphene nanoribbon networks
Sofia Sanz¹, N. Papior², G. Giedke^3,4, D. Sánchez-Portal⁵, M. Brandbyge¹, and T. Frederiksen^3,4

1 Department of Physics, DTU, DK-2800 Kgs. Lyngby, Denmark
2 DTU Computing Center DK-2800 Kgs. Lyngby, Denmark
3 DIPC, E-20018, Donostia-San Sebastián, Spain
4 IKERBASQUE, Basque Foundation for Science, E-48013, Bilbao, Spain
5 CFM-CSIC-UPV/EHU, E-20018, Donostia-San Sebastián, Spain

The similarities between electrons traveling ballistically in graphene nanostructures and photons propagating in waveguides has spawned the novel field of electron quantum optics in graphene constrictions. With the ideas of optics-like experiments in mind, we can think of performing electron interferometry in graphene constrictions, for which some elementary building blocks, e.g., such as electron beam splitters, mirrors, etc., are needed. Remarkably, it has been recently shown that electrons injected in devices formed of two infinite graphene nanoribbons (GNR) placed one on top of the other with a crossing angle of 60º can be split into two outgoing waves without reflection [1-3]. Moreover, GNRs with zigzag edge topology are expected to host spin polarized states due to magnetic instabilities of the localized states at the edges [4], which make these devices even more interesting since we can think of performing both electron and spin quantum optics experiments [5]. With the advent of on-surface synthesis techniques, now not only atomistic defect-free samples of GNRs can be produced [6,7] but also they can be manipulated.

In this work we propose interesting networks for studying electron and spin quantum interferometry built from four crossed GNRs in a pairwise setup (see Figure 1) that splits the beam into two possible paths that will self-interfere at the outgoing ports, where, the resulting interference pattern can be further tuned by an external magnetic field [8] as a consequence of the Aharonov-Bohm effect [9].

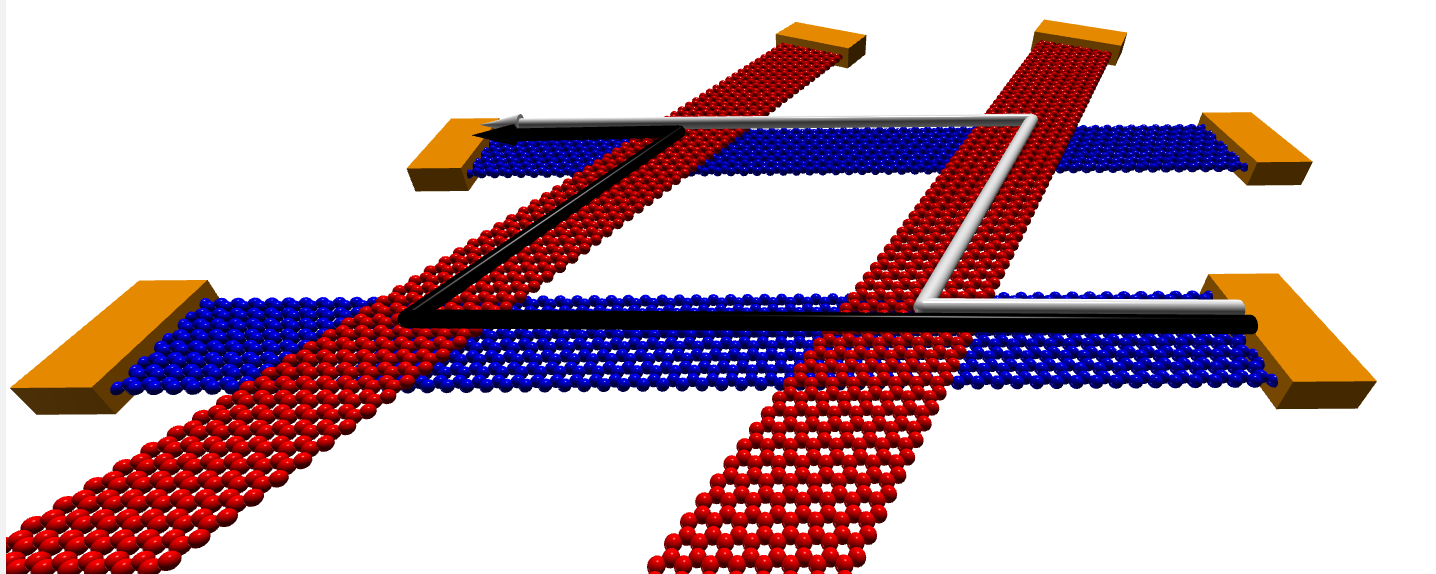Figure 1: Geometry of GNR-based interferometer with the two interfering paths sketched.

[1] L. R. F. Lima et al., J. Phys.: Condens. Matter 28, 505303 (2016).
[2] P. Brandimarte et al., J. Chem. Phys. 146, 092318 (2017).
[3] S. Sanz et al., Phys. Rev. B 102, 035436 (2020).
[4] Y.-W. Son et al., Nature 444, 347–349 (2006).
[5] S. Sanz et al., Phys. Rev. Lett. 129, 037701 (2022).
[6] J. Cai et al., Nature 466, 470 (2010).
[7] P. Ruffieux et al., Nature 531, 489 (2016).
[8] S. Sanz et al., J. Phys.: Condens. Matter 35, 374001 (2023).
[9] Y. Aharonov and D. Bohm, Phys. Rev. 115, 485–491 (1959).